性能
工作应力
压缩波形弹簧产生与弯曲简单横梁类似的弯曲应力。 这些压缩和拉伸应力限制弹簧在 屈服 或"成套"之前可以压缩的量。 虽然弹簧组有时是不能接受的,但符合和偏转要求往往会随着时间的推移带动设计接受一些设置或"放松"。
最大化设计应力
静态应用: 由于 Smalley 产品中使用的硬化扁钢丝的延伸率,Smalley 利用在标准弹簧表中找到的 最小抗张强度 ,该强度接近屈服强度。 当设计用于静态应用的弹簧时,我们推荐计算的工作应力不大于最小抗张强度的 100%。 然而,根据特定的应用,工作应力可以在考虑到屈服强度的情况下超出最小抗张强度。 要考虑的典型因素是永久变形、松弛、负荷和/或自由高度的损失。
动态应用: 当为动态应用设计波形弹簧时,Smalley 建议操作应力的计算值不超过 80% 的最小抗张强度。
残余应力和预置
增加的负荷能力和/或疲劳寿命可以通过压缩弹簧超出其屈服点或"预置"来实现。 预置弹簧被制造为高于所需的自由高度和负荷,然后压缩到极点。 自由高度和负荷降低,材料表面现在显示出残余应力,这就提高弹簧的性能。
疲劳
疲劳周期是在波形弹簧设计的重要考虑事项,可用于精准确定弹簧偏转量如何极大地影响弹簧的价格。 分析应包括弹簧是否偏转全行程或个周期仅有千分之几,或者可能组合两者作为零件磨损或温度变化的原因。
公式:
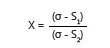
| 疲劳应力比率 | 估计的使用周期 |
| .00 < X < .40 | 30,000 个周期以下 |
| .40 < X < .49 | 30,000 - 50,000 个周期 |
| .50 < X < .55 | 50,000 - 75,000 个周期 |
| .56 < X < .60 | 75,000 - 100,000 个周期 |
| .61 < X < .67 | 100,000 - 200,000 个周期 |
| .68 < X <.70 | 200,000 - 1,000,000 个周期 |
| .70 < X | 超出 1,000,000 个周期 |
术语
σ = 材料抗张强度
S1 = 较低工作高度下的计算工作应力
S2 = 较高工作高度下的计算工作应力
可以在 单层波形弹簧、 对顶®波簧 以及 层叠波簧 页面上使用计算器快速了解工作应力和近似使用周期。
负荷/偏转
实际弹性比率与理论(计算)弹性比率的比较提供了实用的弹簧工作范围限制。 弹性比率 (P/f) 可以通过操作偏转等式进行计算。 通常情况下,在弹簧接近并到达其"压并高度"之前,其理论比率是准确的。
作为一般规则,通过前 80% 的偏转计算出的弹性比率是线性的,而工作高度下降到两倍的压并高度。 虽然弹簧可以超出这个"线性"范围工作,但测量的负荷将大大高于计算值。
可以在相关页面上找到 单层间隙或搭口、 多层(对顶)Spirawave 和 层叠 Spirawave 零件的更多信息。
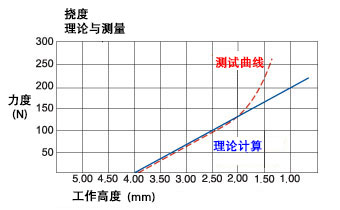
迟滞现象
波形弹簧在装载施加较大的力,而在卸载时施加较小的力。 这种效果称为迟滞现象。 阴影区域显示了曲线之间的图形表示。
在一个单层弹簧中,由于周向和径向运动产生的摩擦是首要原因。 对顶和层叠弹簧也会产生摩擦损耗,因此相邻层之间会产生摩擦。 充分的润滑可最大程度减少这种效果。

直径膨胀
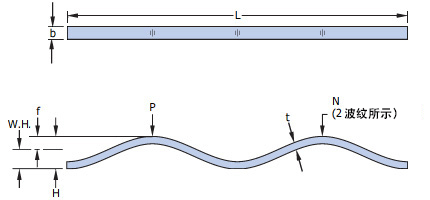
仅限对顶和层叠 Spirawaves: 多层 Spirawaves 在压缩时会直径膨胀。 下面的公式用于预测最大完全压缩直径。
公式:


术语
ODM = 压并时的外径 (in)
R = 波形半径 (in) = (4Y2 + X2)/8Y
N = 波数
θ = 角度 = ArcSin[X/(2R)] (degrees)
b = 径向壁 (in)
X = 1/2 波频率 = (πDM)/(2N)
Y = 1/2 平均自由高度 = (H-t)/2
,其中 H = 每层的自由高度 (in)
线形弹簧
Smalley 线形弹簧是采用弹簧回火材料生产的连续波形(波浪形)长度钢丝。 它们充当负荷轴承设备,其具有与波形弹簧基本相同的负荷/偏转特征。
根据安装位置沿轴向或径向施加力。 沿直线方向压平扩张件,即可产生轴向压力。 圆形包裹扩张件可产生径向力或向外的压力(例如围绕柱塞)。



关注我们